| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Flutter
- system hacking
- Stream
- BOF
- Image Processing
- Computer Architecture
- Got
- llm을 활용 단어장 앱 개발일지
- ARM
- FastAPI
- study book
- Kaggle
- BFS
- Algorithm
- bloc
- MDP
- MATLAB
- Dreamhack
- ML
- pytorch
- DART
- fastapi를 사용한 파이썬 웹 개발
- 백준
- C++
- Widget
- BAEKJOON
- 파이토치 트랜스포머를 활용한 자연어 처리와 컴퓨터비전 심층학습
- rao
- 영상처리
- PCA
- Today
- Total
Bull
[RL] MDP: 모델 기반 (Model-Based) (MDP를 알 때) 본문
[RL] MDP: 모델 기반 (Model-Based) (MDP를 알 때)
Bull_ 2024. 3. 24. 00:10이 포스팅은 학교수업과 노승은 저자의 "바닥부터 배우는 강화 학습"을 바탕으로 정리했다.
학교 수업또한 저자 책을 바탕으로 수업을 받기 때문에 강의자료(요약에 가까운)와 책을 보며 정리했다.
밸류 평가하기 - 반복적 정책 평가
에피소드마다 밸류를 평가해주면서 정책을 업데이트 해준다.
지속적인 업데이트를 하여 실제 값에 가까워진다.
벨만 기대 방정식을 사용하여 예시를 들어보겠다.
기대 방정식과 최적 방정식의 차이는 * 유무를 확인하면된다. (*있는 게 최적 방정식)

그리드 월드의 MDP 정보
• 모든 상태 𝑠에서의 보상: $r^a_s = −1$
• 모든 상태 𝑠에서의 전이 확률: $𝑃^a_{𝑠𝑠′}= 1.0$
• 감쇠 인자: $γ = 1$
• 정책 : 4방향 랜덤
$v_π(s) = \sum_{a∈A} π(a|s)(r^a_s + γ\sum_{s'∈S}P^a_{ss'}v_π(s'))$

모든 상태의 보상을 0으로 초기화하였다.
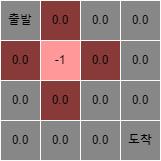
이제 $s_5$에 대하여 공식을 적용해보겠다.
$v_π(s) = \sum_{a∈A} π(a|s)(r^a_s + γ\sum_{s'∈S}P^a_{ss'}v_π(s'))$
$v_π(s_5) = 0.25 * ( -1 + 0.0) + 0.25 * ( -1 + 0.0) + 0.25 * ( -1 + 0.0) + 0.25 * ( -1 + 0.0) = -1.0$
여기서 0.0은 다음 s에 대한 전이확률 * 가치이다.

모든 s를 업데이트 해주면 이제 다시 어느 정도의 수렴값이 보일 때 까지 가치 평가를 해준다.

이제 어느 정도 수렴 값이 보이니 업데이트를 그만 해준다.
보상이 높은 쪽으로 이동할수록 도착지점과 가깝게 찾아갈 수 있다.
최고의 정책 찾기 - 정책 이터레이션
위에서 찾은 가치 값으로 최고의 정책 이터레이션을 제시할 수 있다.
쉽게 말하자면 가치가 낮은 곳에서 높은 쪽으로 액션 방향을 제시해 주는 것이다.

이러한 정책을 Greedy Policy(그리디 정책) 이라고한다. 먼 미래를 생각하지 않고
다음 칸의 가치가 가장 큰 것을 선택하는 것.
이러면 맨 처음 랜덤 정책 $π$에서 그리디 정책 $π'$으로 개선 된 것이다.
평가와 개선 반복
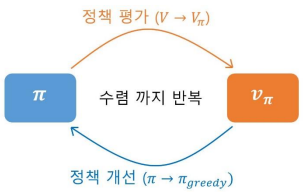
위에서 일정 수렴 밸류를 찾은 후 정책을 평가 해주고 다시 밸류를 업데이트하는 행동을 반복한다.
(정책 평가 → 정책 개선)
반복적으로 정책 평가와 개선을 진행하면 정책과 가치가 변하지 않는 단계에 도달하게 되고,
그 값이 최적 정책과 최적 가치가 된다.

정책 평가를 간소화 하기 위해 평가를 한 번만 진행하고 개선을 바로해주는 방식도 있다.

이렇게 과도하게 평가를 하지 않고 빠르게 최적 정책을 찾을 수 있다.
최고의 정책 찾기 - 밸류 이터레이션
최적 정책이 만들어 낸 최적 밸류를 찾는 것이다.
방법은 똑같다. 하지만 이번에는 최적 방정식을 이용하여 업데이트 해볼 것이다.

$v^*(s) = max_a(r^a_s + γ\sum_{ss'}P^a_{ss'} v^*(s'))$
$ = max(-1 + 1.0 * 0, -1 + 1.0 * 0, -1 + 1.0*0, -1 + 1.0*0)$
$=-1.0$
여기서 전이 확률 $P^a_{ss'}$은 1이다.
동, 서, 남, 북 네 가지 액션에 대한 계산 값 중 최댓값을 사용한 것이다.

최적 밸류를 통해 최적 정책을 알 수 있다.
밸류 이터레이션과 정책 이터레이션의 차이점이라면,
밸류 이터레이션은 정책 개선과 평가를 하지 않고 바로 최선의 정책을 찾아낸 것이다.
'Artificial Intelligence > Reinforcement Learning' 카테고리의 다른 글
| [RL] n-step TD 구현하기 (0) | 2024.03.29 |
|---|---|
| [RL] 벨만 방정식 (with MDP) (1) | 2024.03.23 |
| [RL] MDP(Markov Decision Process) (1) | 2024.03.23 |




